Fadenpendel
- Physik Q2 (sp, 10.03.2016)
Exkurs: harmonische Schwingung I
Was versteht man unter einer harmonischen Schwingung?
- Antwort 1: Die Ort-Zeit-Funktion x(t) einer harmonischen Schwingung ist eine trigonometrische Funktion (→ Sinus oder Cosinus)
Exkurs: harmonische Schwingung II
Was versteht man unter einer harmonischen Schwingung?
- Antwort 2: Kennzeichen einer harmonischen Schwingung → lineare Rückstellkraft (→ hookesches Gesetz!): F = - k⋅x
F = - k⋅x und F = m⋅a → m⋅a = - k⋅x → mx''(t) = -kx(t)
Differenzialgleichung → Abkürzung DGL
ω02 = $\frac{k}{m}$ → DGL: x''(t) + ω02 x(t) = 0
Einsetzen von x(t) = sin (ω0t) → x(t) ist Lösung der DGL.
Bezeichnungen beim Fadenpendel I
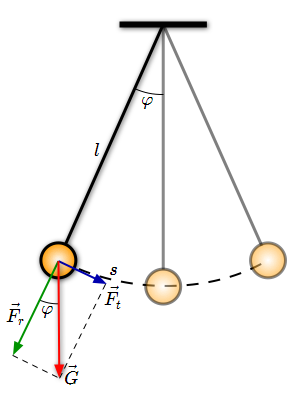
Bezeichnungen beim Fadenpendel II
Bedeutung der Größen in der Abbildung
- s ist ein Kreisbogen. Für den Kreisbogen s gilt: s = l ⋅ φ (wegen φ ⁄ 180° = s ⁄ π⋅r mit l=r)
- l: Länge des Fadens (auch r)
- Winkel φ: um diesen Winkel wird das Fadenpendel ausgelenkt.
- Die Kraft G senkrecht nach unten ist die Gravitationskraft: G = mg
Bezeichnungen beim Fadenpendel III
Bedeutung der Größen in der Abbildung
- Die Schwerkraft G wird zerlegt (Kräfteparallelogramm!) in eine zur Bahn tangentiale Komponente (in Richtung der Kreisbahn) Ft, sowie in eine
- radiale Komponente in Richtung des Radius (= Faden): Fr
- Der radialen Komponente entgegengerichtet ist die Spannkraft des Fadens (fehlt in der Zeichnung!)
Fadenpendel: Analyse I
-
Für die tangentiale Komponente Ft gilt:
Ft = G ⋅ sin φ = m ⋅ g ⋅ sin φ (1) - → rücktreibende Kraft Ft ist wg. der Sinusfunktion nicht proportional zur Auslenkung φ.
- → Die Bewegung des Fadenpendels ist keine harmonische Schwingung!
Fadenpendel: Analyse II
- Für kleine Winkel φ (φ ≤ 15°) können wir für den Quotienten sin φ ⁄ φ ansetzen:
$$ \frac {sin \phi} { \phi} \approx 1$$ - Beachte: Die Näherung gilt nur für φ im Bogenmaß!
Fadenpendel: Analyse III
- Für kleine (!) Auslenkungen φ (φ ≤ 15°) gilt also:
Ft ≈ - m⋅g⋅φ = - s ⋅ mg ⁄ l = - s ⋅ k (2) - Hier wurde $$ k = \frac {m \cdot g} { l} $$ gesetzt.
- Dann ist $$ \frac {k} {m} = \frac {g} {l} $$
Fadenpendel: Analyse IV
- Für kleine (!) Auslenkungen φ (φ ≤ 15°) gilt dann $$ \omega~^2 = \frac {g} {l} $$
- mit ω = 2πf = $\frac {2\pi}{T}$ ergibt sich: $ T = 2 \pi \cdot \sqrt{\frac{l}{g}} $
- D. h.: beim Fadenpendel ist die Periodendauer T abhängig von der Fadenlänge l, jedoch unabhängig von der Masse m!
Quellen
- Der Abschnitt zum Fadenpendel ist eine Zusammenfassung der Kursthemen Physik: Schwingungen und Wellen, Optik, S. 5 - 7.
- Die Bild am Anfang stammt aus Wikipedia, die Abbildung mit den Bezeichnungen des Fadenpendels stammt von Walter Bislins.
Ende
- Präsentation erstellt mit Reveal.js
- →Zurück zur Startseite . . .