(%i1) "Neue Wege Lineare Algebra / Analytische Geometrie"$
(%i2) "Oktaeder-Aufgabe, S, 145/Nr. 17"$
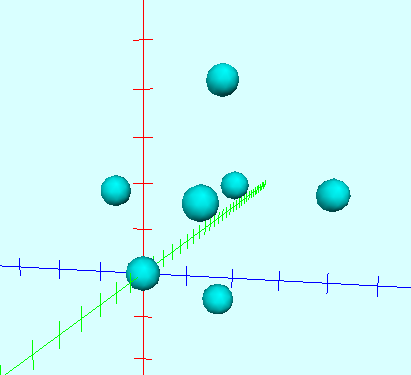
(%i3) "(1) Koordinaten des Oktaeders"$
(%i4) "Punkt A"$
(%i5) A: transpose(matrix ([2.0,0.0,2.0]));
[ 2.0 ]
[ ]
(%o5) [ 0.0 ]
[ ]
[ 2.0 ]
(%i6) "Punkt B"$
(%i7) B: transpose(matrix ([4.0,2.0,2.0]));
[ 4.0 ]
[ ]
(%o7) [ 2.0 ]
[ ]
[ 2.0 ]
(%i8) "Punkt C"$
(%i9) C: transpose(matrix ([2.0,4.0,2.0]));
[ 2.0 ]
[ ]
(%o9) [ 4.0 ]
[ ]
[ 2.0 ]
(%i10) "Punkt D"$
(%i11) D: transpose(matrix ([0.0,2.0,2.0]));
[ 0.0 ]
[ ]
(%o11) [ 2.0 ]
[ ]
[ 2.0 ]
(%i12) "Punkt S_1"$
(%i13) S_1: transpose(matrix ([2.0,2.0,4.0]));
[ 2.0 ]
[ ]
(%o13) [ 2.0 ]
[ ]
[ 4.0 ]
(%i14) "Punkt S_2"$
(%i15) S_2: transpose(matrix ([2.0,2.0,0.0]));
[ 2.0 ]
[ ]
(%o15) [ 2.0 ]
[ ]
[ 0.0 ]

(%i16) "(2) Seitenflächen sind gleichseitige Dreiecke"$
(%i17) "Zeige AB = AS_1 = BS_1"$
(%i18) "Vektor v_AS_1"$
(%i19) v_AS_1: transpose(matrix ([2.0,2.0,4.0])) - transpose(matrix ([2.0,0.0,2.0]));
[ 0.0 ]
[ ]
(%o19) [ 2.0 ]
[ ]
[ 2.0 ]
(%i20) "Vektor v_BS_1"$
(%i21) v_BS_1: transpose(matrix ([2.0,2.0,4.0])) - transpose(matrix ([4.0,2.0,2.0]));
[ - 2.0 ]
[ ]
(%o21) [ 0.0 ]
[ ]
[ 2.0 ]
(%i22) "Vektor v_AB"$
(%i23) v_AB: transpose(matrix ([4.0,2.0,2.0])) - transpose(matrix ([2.0,0.0,2.0]));
[ 2.0 ]
[ ]
(%o23) [ 2.0 ]
[ ]
[ 0.0 ]
(%i24) "Länge der Vektoren:"$
(%i25) "Länge l des Vektors v_AB: l = 2.82842712475"$
(%i26) "Länge l des Vektors v_AS_1: l = 2.82842712475"$
(%i27) "Länge l des Vektors v_BS_1: l = 2.82842712475"$
(%i28) "(3) Winkel zw. Kante BC und Seitenflaeche ABS_1"$
(%i29) "Zwei Punkte A, B der Gerade g"$
(%i30) A : transpose(matrix ([4.0,2.0,2.0]));
[ 4.0 ]
[ ]
(%o30) [ 2.0 ]
[ ]
[ 2.0 ]
(%i31) B : transpose(matrix ([2.0,4.0,2.0]));
[ 2.0 ]
[ ]
(%o31) [ 4.0 ]
[ ]
[ 2.0 ]
(%i32) "Aufpunkt stuetzvec"$
(%i33) stuetzg_BC : transpose(matrix ([4.0,2.0,2.0]));
[ 4.0 ]
[ ]
(%o33) [ 2.0 ]
[ ]
[ 2.0 ]
(%i34) "Richtungsvektor uvec"$
(%i35) uvecg_BC : B - A;
[ - 2.0 ]
[ ]
(%o35) [ 2.0 ]
[ ]
[ 0.0 ]
(%i36) "x-Vektor xvec"$
(%i37) xvec : transpose(matrix ([x,y,z]));
[ x ]
[ ]
(%o37) [ y ]
[ ]
[ z ]
(%i38) "Drei Punkte A, B, C der Ebene"$
(%i39) A : transpose(matrix ([2.0,2.0,4.0]));
[ 2.0 ]
[ ]
(%o39) [ 2.0 ]
[ ]
[ 4.0 ]
(%i40) B : transpose(matrix ([2.0,0.0,2.0]));
[ 2.0 ]
[ ]
(%o40) [ 0.0 ]
[ ]
[ 2.0 ]
(%i41) C : transpose(matrix ([4.0,2.0,2.0]));
[ 4.0 ]
[ ]
(%o41) [ 2.0 ]
[ ]
[ 2.0 ]
(%i42) "Aufpunkt stuetzvec"$
(%i43) stuetzE_ABS_1 : transpose(matrix ([2.0,2.0,4.0]));
[ 2.0 ]
[ ]
(%o43) [ 2.0 ]
[ ]
[ 4.0 ]
(%i44) "Richtungsvektoren uvec und vvec"$
(%i45) uvecE_ABS_1 : B - A;
[ 0.0 ]
[ ]
(%o45) [ - 2.0 ]
[ ]
[ - 2.0 ]
(%i46) vvecE_ABS_1 : C - A;
[ 2.0 ]
[ ]
(%o46) [ 0.0 ]
[ ]
[ - 2.0 ]
(%i47) "Ebenengleichung"$
(%i48) display(stuetzE_ABS_1 + r * uvecE_ABS_1 + s * vvecE_ABS_1)$
[ 2.0 ] [ 0.0 ] [ 2.0 s ] [ 2.0 s + 2.0 ]
[ ] [ ] [ ] [ ]
[ 2.0 ] + [ - 2.0 r ] + [ 0.0 ] = [ 2.0 - 2.0 r ]
[ ] [ ] [ ] [ ]
[ 4.0 ] [ - 2.0 r ] [ - 2.0 s ] [ - 2.0 s - 2.0 r + 4.0 ]
(%i49) "Schnittpunkt der Gerade g_BC und der Ebene E_ABS_1"$
(%i50) sp : transpose(matrix([ 4.00000000000000, 2.00000000000000, 2.00000000000000]));
[ 4.0 ]
[ ]
(%o50) [ 2.0 ]
[ ]
[ 2.0 ]
(%i51) "Schnittwinkel alpha = 54.735610317245"$
(%i52) "(4) Blickwinkel vom Punkt B aus"$
(%i53) "a) Blickwinkel zw. BC und BD"$
(%i54) "Vektor v_BC"$
(%i55) v_BC: transpose(matrix ([2.0,4.0,2.0])) - transpose(matrix ([4.0,2.0,2.0]));
[ - 2.0 ]
[ ]
(%o55) [ 2.0 ]
[ ]
[ 0.0 ]
(%i56) "Vektor v_BD"$
(%i57) v_BD: transpose(matrix ([0.0,2.0,2.0])) - transpose(matrix ([4.0,2.0,2.0]));
[ - 4.0 ]
[ ]
(%o57) [ 0.0 ]
[ ]
[ 0.0 ]
(%i58) "Winkel zwischen Vektor v_BC und Vektor v_BD: alpha = 45.0000000000"$
(%i59) "b) Blickwinkel zw. BD und BS_2"$
(%i60) "Vektor v_BS_2"$
(%i61) v_BS_2: transpose(matrix ([2.0,2.0,0.0])) - transpose(matrix ([4.0,2.0,2.0]));
[ - 2.0 ]
[ ]
(%o61) [ 0.0 ]
[ ]
[ - 2.0 ]
(%i62) "Winkel zwischen Vektor v_BD und Vektor v_BS_2: alpha = 45.0000000000"$
(%i63) "(5) Gleichung für E deuten"$
(%i64) "Aufpunkt stuetzE_5"$
(%i65) stuetzE_5 : transpose(matrix ([4.0,2.0,2.0]));
[ 4.0 ]
[ ]
(%o65) [ 2.0 ]
[ ]
[ 2.0 ]
(%i66) "Richtungsvektoren uvec und vvec"$
(%i67) uvecE_5 : transpose(matrix ([-2.0,2.0,0.0]));
[ - 2.0 ]
[ ]
(%o67) [ 2.0 ]
[ ]
[ 0.0 ]
(%i68) vvecE_5 : transpose(matrix ([-2.0,0.0,2.0]));
[ - 2.0 ]
[ ]
(%o68) [ 0.0 ]
[ ]
[ 2.0 ]
(%i69) "Ebenengleichung"$
(%i70) display(stuetzE_5 + r * uvecE_5 + s * vvecE_5)$
[ 4.0 ] [ - 2.0 r ] [ - 2.0 s ] [ - 2.0 s - 2.0 r + 4.0 ]
[ ] [ ] [ ] [ ]
[ 2.0 ] + [ 2.0 r ] + [ 0.0 ] = [ 2.0 r + 2.0 ]
[ ] [ ] [ ] [ ]
[ 2.0 ] [ 0.0 ] [ 2.0 s ] [ 2.0 s + 2.0 ]
(%i71) "Die Ebene E_5 geht durch die Punkte B, C und S_1"$
(%i72) "und enthält die Seitenfläche BCS_1"$
(%i73) "(6) Werte für r und s einschränken"$
(%i74a) "Beachte: (I) 0 <= r, s <= 1 entspricht einem Quadrat!"$
(%i74b) "Bedingung: (I) + (II) r + s = 1 (Nachweis?)"$
(%i75) "(7) Welcher Winkel wurde bestimmt?"$
(%i76) "Winkel zw. Vektor BC und Vektor (-2|-2|0)^T"$
(%i77) "Vektor (-2|-2|0)^T = AB"$
(%i78) "D. h. der Winkel entspricht dem Winkel zw. AB und BC"$
(%i79) "Winkel zwischen Vektor v_AB und Vektor v_BC: alpha = 90.0000000000"$
(%i80) "(8) Weitere Winkel . . ."$
(%i81) "Überlege selbst!"$